module Vector.Vector where
import Test.QuickCheck hiding (scale)

Vectors in two dimensions.

A physical quantity that has only a magnitude is called a scalar. In Haskell we’ll represent this using a Double.

type Scalar = Double

A vector is a quantity that has both a magnitude and a direction. For instance the velocity of a moving body involves its speed (magnitude) and the direction of motion.

We cen represent the direction of a vector in two dimensions using its \(x\) and \(y\) coordinates, which are both scalars. The direction is then given by the angle between these coordinates and the origin (0,0).

In order to maintain generalizability and useability in the next chapters we’ll use a typesynonym in the data declaration but throughout this whole chapter we’ll use Scalars as we’ve defined them here.

data Vector2 num = V2 num num

We can even introduce a type that makes that specific relationship clearer:

type VectorTwo = Vector2 Scalar

The magnitude of the vector is it’s length. We can calculate this using Pythagorean theorem: \[\begin{equation} x^2 + y^2 = magnitude^2 \end{equation}\]

In haskell this would be:

magnitude :: VectorTwo -> Scalar
magnitude (V2 x y) = sqrt (x^2 + y^2)

And now we can calulate the magnitude of a vector in two dimensions:

  Vector> let vec = V2 5 3
  Vector> magnitude vec
  5.830951894845301

Addition and subtraction of vectors is accomplished using the components of the vectors. For instance when adding the forces (vectors) acting on a body we would add the components of the forces acting in the \(x\) direction and the components in the \(y\) direction. So our functions for adding and subtracting vectors in two dimensions are:

add :: VectorTwo -> VectorTwo -> VectorTwo
add (V2 x1 y1) (V2 x2 y2) = V2 (x1 + x2) (y1 + y2)

sub :: VectorTwo -> VectorTwo -> VectorTwo
sub (V2 x1 y1) (V2 x2 y2) = V2 (x1 - x2) (y1 - y2)

But this only works for two vectors. In reality we might be working with several hundreds of vectors so it would be useful to add, for instance a list of vectors together and get one final vector as a result. We can use foldr using the zero vector as a starting value. to acomplish this.

zeroVector :: VectorTwo
zeroVector = V2 0 0

addListOfVectors :: [VectorTwo] -> VectorTwo
addListOfVectors = foldr add zeroVector

Let’s try it out!

  *Vector> let vec1 = V2 5 3
  *Vector> let vec2 = V2 6 5
  *Vector> sub vec1 vec2

  <interactive>:23:1: error:
      • No instance for (Show VectorTwo) arising from a use of ‘print’
      • In a stmt of an interactive GHCi command: print it

The interpreter is complaining that it doesn’t know how to interpret our datatype for vectors as a string. The easy solution would be to just derive our instance for Show, but to really solidify the fact that we are working with coordinates let’s make our own instance for Show.

instance Show num => Show (Vector2 num) where
  show (V2 x y) = "(" ++ show x ++ ", " ++ show y ++ ")"

And let’s try our example again:

  *Vector> let vec1 = V2 5 3
  *Vector> let vec2 = V2 6 5
  *Vector> sub vec1 vec2
  (-1 x, -2 y)

And let’s also try adding a list of vectors using our new function:

  *Vector> let vec3 = V2 8 9
  *Vector> let vectors = [vec1, vec2, vec3]
  *Vector> addListOfVectors vectors
  (19.0 x, 17.0 y)

It works!

We can also multiply a vector by a scalar. This is also done componentwise. We’ll call this scaling a vector. So we could double a vector by multiplying it with \(2.0\) and halving it by multiplying it with \(0.5\).

scale :: Scalar -> VectorTwo -> VectorTwo
scale factor (V2 x y) = V2 (factor * x) (factor * y)

Combining this with the unit vectors:

unitX :: VectorTwo
unitX = V2 1 0

unitY :: VectorTwo
unitY = V2 0 1

We get a new way of making vectors, namely by scaling the unit vectors and adding them together. Let’s create the vector (5 x, 3 y) using this approach.

  *Vector> add (scale 5 unitX) (scale 3 unitY)
  (5.0 x, 3.0 y)

In order to check that this vector is actually equal to the vector created using the contructor V2 we need to make our vector an instance of Eq.

instance Eq num => Eq (Vector2 num) where
  (V2 x1 y1) == (V2 x2 y2) = (x1 == x2) && (y1 == y2)

Let’s try it out:

  *Vector> let vec1 = V2 5 3
  *Vector> let vec2 =  add (scale 5 unitX) (scale 3 unitY)
  *Vector> vec1 == vec2
  True

We have one final important operation left to define for vectors in two dimensions, the dot product. The formula is quite simple: \[\begin{equation} \vec{a} \cdot \vec{b} = a_x \cdot b_x + a_y \cdot b_y \end{equation}\]

And our function simply becomes:

dotProd :: VectorTwo -> VectorTwo -> Scalar
dotProd (V2 ax ay) (V2 bx by) = ax * bx + ay * by

But this doesn’t give us any intuition about what it means to take the dot product between vectors. The common interpretation is “geometric projection”, but that only makes sense if you already understand the dot product. Let’s try to give an easier analogy using the dash panels (boost pads) from Mario Kart. The dash panel is designed to give you boost of speed in a specific direction, usually straight forward. So the vector associated with the dash panel can be represented with a unit vector multiplied with some factor of boost, say 10.

dashPanel :: VectorTwo
dashPanel = scale 10 unitY

Now let’s say that your cart has this arbitrarily chosen velocity vector:

cart :: VectorTwo
cart = V2 3 5

Depending on which angle you hit the dash panel you’ll receive different amounts of boost. Since the \(x\)-component of the dashPanel is 0 any component of speed on the \(x\)-direction will be reduced to zero. Only the speed in the direction of \(y\) will be boosted. But there are worse ways to hit the dash panel. We could for instance create a new velocity vector with the exact same magnitude of speed but which would recieve a worse boost.

worseCart :: VectorTwo
worseCart = V2 5 3

Let’s see this in action.

*Vector> magnitude cart == magnitude worseCart
True
*Vector> dotProd dashPanel cart
50.0
*Vector> dotProd dashPanel worseCart
30.0

We talked a lot about angles between vectors but we havn’t used it in our code, so lets make a function which calculates the angle of a vector. The formula is as follows:

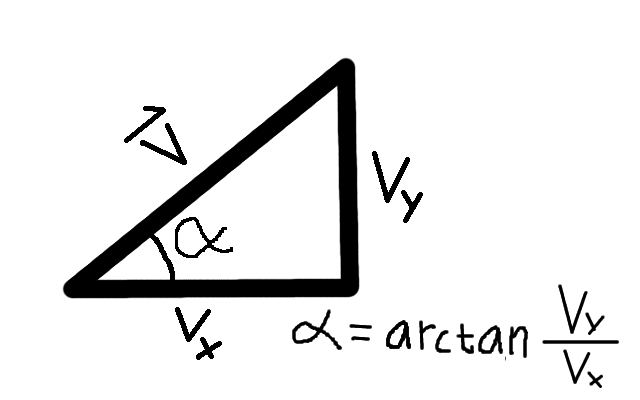
We’ll use Doubles to represent the angle.

type Angle  = Double

angle :: VectorTwo -> Scalar
angle (V2 x y) = atan y/x

Using angles and magnitudes we can even write a new function for making vectors:

mkVector :: Scalar -> Angle -> VectorTwo
mkVector mag angle = V2 x y
  where
    x = mag * cos angle
    y = mag * sin angle

Vectors in three dimensions.

The datatype for a vector in three dimensions is basically the same as vector in two dimensions, we’ll just add a \(z\)-component.

Again we will generalize this over a type synonym

data Vector3 num = V3 num num num

And a type synonym that we can use throughout the rest of this chapter.

type VectorThree = Vector3 Scalar

Similarily the functions for adding three dimensional vectors:

add :: VectorThree -> VectorThree -> VectorThree
add (V3 x1 y1 z1) (V3 x2 y2 z2) = V3 (x1 + x2) (y1 + y2) (z1 + z2)

Multiplying with a scalar:

scale3 :: Scalar -> VectorThree -> VectorThree
scale3 fac (V3 x y z) = V3 (fac * x) (fac * y) (fac * z)

And for calculating the magnitude:

mag3 :: VectorThree -> Scalar
mag3 (V3 x y z) = sqrt (x**2 + y**2 + z**2)

Looks earily similar to our functions for vectors in two dimensions. This suggest that there might be a better way to handle this, in order to avoid repeating ourselves.

Addition and subtraction on vectors works by “unpacking” the vectors, taking their components, applying some function to them (+/-) and then packing them up as a new vector. This is very similar to the Haskell function zipWith which works over lists instead of vectors.

zipWith :: (a -> b -> c) -> [a] -> [b] -> [c]

When we’re multiplying with a scalar we again unpack the vector and then apply mulitiplication with a factor to each component before packing it up again. This is quite similar to the Haskell function map, which again works over lists.

map :: (a -> b) -> [a] -> [b]

When calculating the magnitude of a vector we first unpack the vector and then apply \(^2\) to each component of the vector. This is doable with aformentioned map. We then fold the components together using \(+\) which results in a final scalar value. Those of you familliar with functional languages will know where I’m going with this, those of you who aren’t will hopefully understand where I’m going when reading the examples.

Using this information we can now create a new class for vectors which implement this functionality:

class Vector vec where
  vmap      :: (num -> num)         -> vec num -> vec num
  vzipWith  :: (num -> num  -> num) -> vec num -> vec num -> vec num
  vfold     :: (num -> num  -> num) -> vec num -> num

Now we have a blueprint for what vector is, so let’s implement it for our own vector datatypes.

instance Vector Vector2 where
  vmap     f (V2 x y)            = V2 (f x)    (f y)
  vzipWith f (V2 x y) (V2 x' y') = V2 (f x x') (f y y')
  vfold    f (V2 x y)            = f x y

instance Vector Vector3 where
  vmap     f (V3 x y z)               = V3 (f x)    (f y)    (f z)
  vzipWith f (V3 x y z) (V3 x' y' z') = V3 (f x x') (f y y') (f z z')
  vfold    f (V3 x y z)               = f z $ f x y

Now we’re finally leveraging the power of the Haskell typesystem!

We can now implement more generalized functions for addition and subtraction between vectors.

add :: (Num num, Vector vec) => vec num -> vec num -> vec num
add = vzipWith (+)

sub :: (Num num, Vector vec) => vec num -> vec num -> vec num
sub = vzipWith (-)

For multiplying with a scalar:

scale :: (Num num, Vector vec) => num -> vec num -> vec num
scale factor = vmap (* factor)

And for calculating the magnitude of a vector:

magnitude :: (Floating num, Vector vec) => vec num -> num
magnitude = sqrt . vfold (+) . vmap (**2)

We can even use it to make a generalized function for calculating the dot product.

dotProd :: (Num num, Vector vec) => vec num -> vec num -> num
dotProd v1 v2 = vfold (+) $ vzipWith (*) v1 v2

Cross Product

We have one final function left to define, the cross product. The formula is as follows: \[\begin{equation} \vec{a} \times \vec{b} = |\vec{a}| \cdot |\vec{b}| \cdot sin(\theta) \end{equation}\]

Where \(\theta\) is the angle between the vectors. And \(|\vec{a}|\), \(|\vec{b}|\) are the magnitudes of the vectors.

So our function for calculating the cross product becomes:

TODO: Generate normal vector as well. Codify right hand rule

crossProd :: Vector3 -> Vector3 -> Vector3
crossProd a b = (magnitude a) * (magnitude b) * sin (angleBetween a b)
  where
    angleBetween :: (Vector vec) => vec -> vec -> Scalar
    angleBetween v1 v2 = acos ((dotProd v1 v2) / ((magnitude v1) * (magnitude v2)))

Working cross product using matrix rules.

crossProd :: Num num => Vector3 num -> Vector3 num -> Vector3 num
crossProd (V3 x y z) (V3 x' y' z') = V3 (y*z' - z*y') -- X
                                        (z*x' - x*z') -- Y
                                        (x*y' - y*x') -- Z

Quickcheck!

There are certain laws or preperties that vectors adher to, for example the jacobi identity:

Or that the cross product is anticommutative. We can’t actually prove these in a meaningful way without a whole bunch of packages and pragmas, but we can quickcheck them. But to do that we need to be able to generate vectors, so let’s make our vectors an instance of Arbitrary.

We do this by generating arbitrary scalars and then constructing vectors with them.

instance Arbitrary num => Arbitrary (Vector2 num) where
  arbitrary = arbitrary >>= (\(s1, s2) -> return $ V2 s1 s2)

instance Arbitrary num => Arbitrary (Vector3 num) where
  arbitrary = arbitrary >>= (\(s1, s2, s3) -> return $ V3 s1 s2 s3)

Let’s try it out!

ghci> generate arbitrary :: IO (Vector2 Scalar)
(-26.349975377051404 x, 9.71134047527185 y)

Seems pretty random to me.

Now we can check some properties, lets’ start with commutativity of vector addition: \[\begin{equation} \vec{a} + \vec{b} = \vec{b} + \vec{a} \end{equation}\]

Which translates to:

prop_CommutativityAddition :: VectorThree -> VectorThree -> Bool
prop_CommutativityAddition v1 v2 = v1 + v2 == v2 + v1

And we test this in the repl.

ghci> quickCheck prop_CommutativityAddition
+++ OK, passed 100 tests.

And associativity of addition: \[\begin{equation} \vec{a} + (\vec{b} + \vec{c}) = (\vec{a} + \vec{b}) + \vec{c} \end{equation}\]

prop_AssociativityAddition :: VectorThree -> VectorThree -> VectorThree -> Bool
prop_AssociativityAddition a b c = a + (b + c) == (a + b) + c

ghci> quickCheck prop_AssociativityAddition
*** Failed! Falsifiable (after 2 tests):
(0.5240133611343812 x, -0.836882545823441 y, -4776.775557184785 z)
(-0.17261751005585407 x, 0.7893754200476363 y, -0.19757165887775568 z)
(0.3492200657348603 x, 0.10861834028920295 y, 0.45838513657221946 z)

This is very strange since the laws should always be correct. But this error stems from the fact that we’re using a computer and that using doubles (Scalar) will introduce approximation errors. We can fix this by relaxing our instance for Eq and only requiring the components of the vectors to be approximately equal.

% TODO: Equation

eps :: Floating num => num
eps = 1 * (10 ** (-5))

instance (Floating num, Eq num, Ord num) => Eq (Vector2 num) where
  (V2 x1 y1) == (V2 x2 y2) = xCheck && yCheck
    where
      xCheck = abs (x1 - x2) <= eps
      yCheck = abs (y1 - y2) <= eps

Let’s try again.

*Vector.Vector> quickCheck prop_AssociativityAddition
+++ OK, passed 100 tests.

More laws

Dot product is commutative:

prop_dotProdCommutative :: VectorThree -> VectorThree -> Bool
prop_dotProdCommutative a b = dotProd a b == dotProd b a

In order to check some laws which depends on checking the equality of scalars we’ll introduce a function which checks that two scalars are approximately equal.

-- Approx equal
(~=) :: Scalar -> Scalar -> Bool
rhs ~= lhs = abs (rhs - lhs) <= eps

Dot product is distributive over addition:

prop_dotProdDistrubitiveAddition ::  VectorThree -> VectorThree -> VectorThree -> Bool
prop_dotProdDistrubitiveAddition a b c = dotProd a (b + c) ~= (dotProd a b + dotProd a c)

The dot product is homogeneous under scaling in each variable: \[\begin{equation} (x * \vec{a}) \cdot b = x * (\vec{a} \cdot \vec{b}) = \vec{a} \cdot (x * \vec{b}) \end{equation}\]

prop_dotProdHomogeneousScaling :: Scalar -> VectorThree -> VectorThree -> Bool
prop_dotProdHomogeneousScaling x a b = e1 == e2 && e2 == e3
  where
    e1 = dotProd (scale 0 a) b
    e2 = 0 * dotProd a b
    e3 = dotProd a (scale 0 b)

The cross product of a vector with itself is the zero vector.

prop_crossProd_with_self :: VectorThree -> Bool
prop_crossProd_with_self v = crossProd v v == 0

The crossproduct is anticommutative: \[\begin{equation} \vec{a} \times \vec{b} = - (\vec{b} \times \vec{a}) \end{equation}\]

prop_crossProdAntiCommutative :: VectorThree -> VectorThree -> Bool
prop_crossProdAntiCommutative v1 v2 = v1 * v2 == - (v2 * v1)

The cross product is distributive over addition: \[\begin{equation} \vec{a} \times (\vec{b} + \vec{c}) = (\vec{a} \times \vec{b}) + (\vec{a} \times \vec{c}) \end{equation}\]

prop_crossProdDistrubitiveAddition :: VectorThree -> VectorThree -> VectorThree -> Bool
prop_crossProdDistrubitiveAddition a b c = a * (b + c) == (a * b) + (a * c)

Vector triple product (Lagrange’s formula).

prop_lagrange :: VectorThree -> VectorThree -> VectorThree -> Bool
prop_lagrange a b c = a * (b * c) == (scale (dotProd a c) b -
                                      scale (dotProd a b) c)

The Jacobi identity: \[\begin{equation} \vec{a} \times (\vec{b} \times \vec{c}) + \vec{b} \times (\vec{c} \times \vec{a}) + \vec{v} \times (\vec{a} \times \vec{b}) \end{equation}\]

prop_JacobiIdentity :: VectorThree -> VectorThree -> VectorThree -> Bool
prop_JacobiIdentity a b c = a * (b * c) +
                            b * (c * a) +
                            c * (a * b) == 0

Fun instances

instance Num num => Monoid (Vector2 num) where
  mempty  = zeroVector
  mappend = (+)
  mconcat = foldr mappend mempty

instance Num num => Monoid (Vector3 num) where
  mempty  = zeroVector
  mappend = (+)
  mconcat = foldr mappend mempty


instance Num num => Num (Vector2 num) where
  (+)           = vzipWith (+)
  (*)           = undefined -- Crossproduct not defined for Vector2
  abs           = vmap abs
  negate        = vmap (*(-1))
  -- | Signum can be though of as the direction of a vector
  signum        = vmap signum
  fromInteger i = V2 (fromInteger i) 0

instance Num num => Num (Vector3 num) where
  (+)           = vzipWith (+)
  (*)           = crossProd
  abs           = vmap abs
  negate        = vmap (*(-1))
  -- | Signum can be though of as the direction of a vector
  signum        = vmap signum
  fromInteger i = V3 (fromInteger i) 0 0

-- TODO: Explain why this works

zeroVector :: (Vector vec, Num (vec num)) => vec num
zeroVector = 0

instance Show num => Show (Vector3 num) where
  show (V3 x y z) = "(" ++ show x ++ " x, "
                        ++ show y ++ " y, "
                        ++ show z ++ " z)"
instance (Floating num, Ord num) => Ord (Vector2 num) where
  compare v1 v2 = compare (magnitude v1) (magnitude v2)

instance (Floating num, Ord num) => Ord (Vector3 num) where
  compare v1 v2 = compare (magnitude v1) (magnitude v2)

instance (Ord num, Floating num, Eq num) => Eq (Vector3 num) where
  (V3 x y z) == (V3 x' y' z') = xCheck && yCheck && zCheck
    where
    xCheck = abs (x - x') <= eps
    yCheck = abs (y - y') <= eps
    zCheck = abs (z - z') <= eps

runTests :: IO ()
runTests = do
  putStrLn "Commutativity of vector addition:"
  quickCheck prop_CommutativityAddition
  putStrLn "Associativity of vector addition:"
  quickCheck prop_AssociativityAddition
  putStrLn "Dot product distributive over addition:"
  quickCheck prop_dotProdDistrubitiveAddition
  putStrLn "Homogeneous scaling:"
  quickCheck prop_dotProdHomogeneousScaling
  putStrLn "Commutative dot product:"
  quickCheck prop_dotProdCommutative
  putStrLn "Crossproduct of a vector with itself:"
  quickCheck prop_crossProd_with_self
  putStrLn "Cross product is anticommutative"
  quickCheck prop_crossProdAntiCommutative
  putStrLn "Cross product distributive over addition"
  quickCheck prop_crossProdDistrubitiveAddition
  putStrLn "Lagrange formula"
  quickCheck prop_lagrange
  putStrLn "Jacobi identity"
  quickCheck prop_JacobiIdentity