Quantities

module Dimensions.Quantity
    ( Quantity
    , length, mass, time, current, temperature, substance, luminosity, one
    , velocity, acceleration, force, momentum
    , meter, kilogram, second, ampere, kelvin, mole, candela, unitless
    , (~=)
    , isZero
    , (#), (##)
    , (+#), (-#), (*#), (/#)
    , sinq, cosq, asinq, acosq, atanq, expq, logq
    , qfold
    ) where

import qualified Dimensions.ValueLevel as V
import           Dimensions.TypeLevel  as T
import           Prelude               as P hiding (length)

We’ll now create a data type for quantities and combine dimensions on value-level and type-level. Just as before, a bunch of GHC-extensions are necessary.

{-# LANGUAGE UndecidableInstances #-}
{-# LANGUAGE FlexibleInstances #-}
{-# LANGUAGE GADTs #-}
{-# LANGUAGE DataKinds #-}
{-# LANGUAGE TypeOperators #-}
{-# LANGUAGE KindSignatures #-}

So what exactly does a physical “quantity” contain? Have a look at this picture

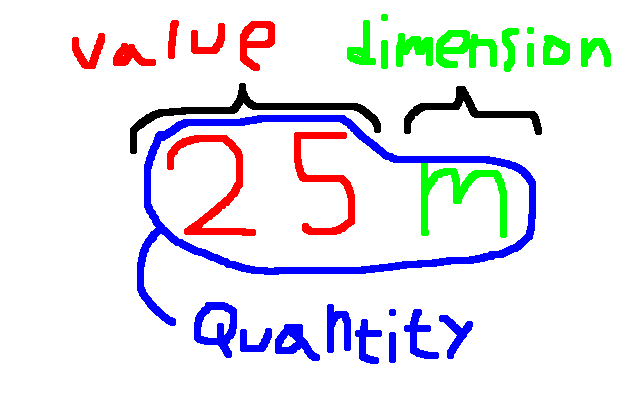
This is what quantities look like in physics calculations. They have a numerical value and a dimension (which is often given by instead writing its unit). The whole thing combined is the quantity. This combined thing is what we want to have a data type for in Haskell.

It’s evident the data type should have a numerical value and a dimension. But so far we have created two dimensions! Which should we use? Both! The value-level dimension of the quantity is used to print it nicely. The type-level dimension of the quantity is to get some type-safety. Just like this \[\begin{align} 25 m + 7 kg = ... \end{align}\] should upset you, this (in pseudo-Haskell)

ghci> let q1 = 25 m -- A value of the quantity type
ghci> let q2 = 7 kg -- Another value of the quantity type
ghci> q1 + q2
...

should upset the compiler!

We can’t cover all everything at once, but we guarantee you that by the end of this chaper, you’ll know exactly how the above ideas are actually implemented.

Let’s get on to the actual data type declaration.

data Quantity (d :: T.Dim) (v :: *) where
  ValQuantity :: V.Dim -> v -> Quantity d v

That was sure a mouthful! Let’s break it down. data Quantity (d :: T.Dim) (v :: *) creates the type constructor Quantity. A type constructor takes types to create another type. In this case, the type constructor Quantity takes a type d of kind T.Dim and a type v of kind * to create the type Quantity d v. Let’s see it in action

type ExampleType = Quantity T.Length Double

ExampleType is the type representing quantites of the physical dimension length and where the numerical value is of the type Double.

How do we create values of this type? That’s where the second row comes in! ValQuantity is a value constructor, which means it takes values to create another value. In this case, the value constructor ValQuantity takes a value of type V.Dim and v. Let’s see this one in action as well

exampleValue = ValQuantity V.length 25.0

exampleValue is a value for the quantity representing a length with the numerical value \(25.0\).

We can combine the two and write this

exampleValue :: ExampleType

or

exampleValue :: Quantity T.Length Double
exampleValue = ValQuantity V.length 25.0

to get the full picture. So, here we are, with a way to create quantity values (ValQuantity) of the type Quantity t1 t2 where t1 is the type-level dimension of the quantity and t2 the type of the numerical value. If you still find it confusing, don’t worry! Over the course of this chapter, it’ll become more concrete as we work more with Quantity.

Also note that the type-level dimension and value-level dimension are intented to match when used with Quantity! So far nothing enforces this. We’ll tackle this problem later.

Exercise create Quantity values for \(2.5\) meters, \(6.7\) seconds and \(9\) mol. Recall that the three mentioned SI-units here, and all SI-units in this tutorial in general, have a one-to-one correspondence with their respective dimension.

theDistance :: Quantity T.Length Double
theDistance = ValQuantity V.length 2.5

theTime :: Quantity T.Time Double
theTime = ValQuantity V.time 6.7

theAmountOfSubstance :: Quantity T.Substance Integer
theAmountOfSubstance = ValQuantity V.substance 9

Exercise Create a data type which has two type-level dimensions, always use Rational as the value-holding type (the role of v) but which has no value-level dimensions. It should have three numerical values. Create some values of that type.

data Quantity' (d1 :: T.Dim) (d2 :: T.Dim) where
  ValQuantity' :: Rational -> Rational -> Rational -> Quantity' d1 d2

val1 :: Quantity' T.Luminosity T.Mass
val1 = ValQuantity' 8 7 3

val2 :: Quantity' T.Substance T.Temperature
val2 = ValQuantity' 2 3 1

Pretty-printer

Let’s do a pretty-printer for quantities. Most of the work is already done by the value-level dimensions.

showQuantity :: (Show v) => Quantity d v -> String
showQuantity (ValQuantity d v) = show v ++ " " ++ show d

instance (Show v) => Show (Quantity d v) where
  show = showQuantity

Exercise In a previous exercise, you created some example values of the Quantity type. Write them in GHCi and see how they look.

ghci> theDistance
2.5 m
ghci> theTime
6.7 s
ghci> theAmountOfSubstance
9 mol

Pretty, huh?

A taste of typos

We’ll implement all arithmetic operations on Quantity, but for now, to get a taste of types, we show here addition and multiplication and some examples of values of type Quantity.

quantityAdd :: (Num v) => Quantity d v ->
                          Quantity d v ->
                          Quantity d v
quantityAdd (ValQuantity d v1) (ValQuantity _ v2) = ValQuantity d (v1+v2)

The type is interpreted as follows: two values of type Quantity d v is the input, where d is the type-level dimension. The output is also a value of type Quantity d v.

The type of the function forces the inputs to have the same dimensions. For this reason, the dimension on value-level doesn’t matter on one of the arguments, because they will be the same. As was already mentioned when the Quantity type was created, it’s possible to create values where the dimensions on value-level and type-level don’t match. Just like then, we ignore this problem for now and fix it later!

Multiplication is implemented as

quantityMul :: (Num v) => Quantity d1 v ->
                          Quantity d2 v ->
                          Quantity (d1 `Mul` d2) v
quantityMul (ValQuantity d1 v1) (ValQuantity d2 v2) =
  ValQuantity (d1 `V.mul` d2) (v1*v2)

The type has the following interpretation: two values of type Quantity dx v is input, where dx are two types representing (potentially different) dimensions. As output, a value of type Quantity is returned. The type in the Quantity will be the type that is the product of the two dimensions in.

Exercise Implement subtraction and division.

Now on to some example values and types.

width :: Quantity T.Length Double
width = ValQuantity V.length 0.5

height :: Quantity T.Length Double
height = ValQuantity V.length 0.3

type Area = Mul T.Length T.Length

The following example shows that during a multiplication, the types will change, as they should. The dimensions change not only on value-level but also on type-level.

area :: Quantity Area Double
area = quantityMul width height

ghci> width
0.5 m
ghci> :t width
width :: Quantity Length Double
ghci> area
0.15 m^2
ghci> :i area
area :: Quantity Area Double

(Try out :t instead of :i on the last one and see what happens!)

The type-level dimensions are used below to enforce, at compile-time, that only allowed operations are attempted.

-- Doesn't even compile
weird = quantityAdd width area

If the dimensions had been value-level only, this error would go undetected until run-time.

Exercise What is the volume of a cuboid with sides \(1.2\ m\), \(0.4\ m\) and \(1.9\ m\)? Create values for the involved quantities. Use Float instead of Double.

side1 :: Quantity Length Float
side1 = ValQuantity V.length 1.2

side2 :: Quantity Length Float
side2 = ValQuantity V.length 0.4

side3 :: Quantity Length Float
side3 = ValQuantity V.length 1.9

type Volume = Length `Mul` (Length `Mul` Length)

volume :: Quantity Volume Float
volume = quantityMul side1 (quantityMul side2 side3)

Comparsions

It’s useful to be able to compare quantities. Perhaps one wants to know which of two amounts of energy is the largest. But what’s the largest of 1 J and 1 m? That’s no meaningful comparsion since the dimensions don’t match. This behaviour is prevented by having type-level dimensions.

quantityEq :: (Eq v) => Quantity d v -> Quantity d v -> Bool
quantityEq (ValQuantity _ v1) (ValQuantity _ v2) = v1 == v2

instance (Eq v) => Eq (Quantity d v) where
  (==) = quantityEq

Exercise Make Quantity an instance of Ord.

quantityCompare :: (Ord v) => Quantity d v ->
                              Quantity d v -> Ordering
quantityCompare (ValQuantity _ v1) (ValQuantity _ v2) =
  compare v1 v2

instance (Ord v) => Ord (Quantity d v) where
  compare = quantityCompare

We often use Double as the value holding type. Doing exact comparsions isn’t always possible to due rounding errors. Therefore, we’ll create a ~= function for testing if two quantities are almost equal.

infixl 4 ~=
(~=) :: Quantity d Double -> Quantity d Double -> Bool
(ValQuantity _ v1) ~= (ValQuantity _ v2) = abs (v1-v2) < 0.001

Testing if a quantity is zero is something which might be a common operation. So we define it here.

isZero :: (Fractional v, Ord v) => Quantity d v -> Bool
isZero (ValQuantity _ v) = abs v < 0.001

Arithmetic on quantities

Let’s implement the arithmetic operations on Quantity. Basically it’s all about creating functions with the correct type-level dimensions.

infixl 6 +#
(+#) :: (Num v) => Quantity d v -> Quantity d v ->
                   Quantity d v
(+#) = quantityAdd

infixl 6 -#
(-#) :: (Num v) => Quantity d v -> Quantity d v ->
                   Quantity d v
(ValQuantity d v1) -# (ValQuantity _ v2) = ValQuantity d (v1-v2)

infixl 7 *#
(*#) :: (Num v) => Quantity d1 v -> Quantity d2 v ->
                   Quantity (d1 `Mul` d2) v
(*#) = quantityMul

infixl 7 /#
(/#) :: (Fractional  v) => Quantity d1 v ->
                           Quantity d2 v ->
                           Quantity (d1 `Div` d2) v
(ValQuantity d1 v1) /# (ValQuantity d2 v2) =
  ValQuantity (d1 `V.div` d2) (v1 / v2)

For all operations on quantities, one does the operation on the value and, in the case of multiplication and division, on the dimensions separetly. For addition and subtraction the in-dimensions must be the same. Nothing then happens with the dimension.

How does one perform operations such as sin on a quantity with a potential dimension? The answer is that the quantity must be dimensionless, and with the dimension nothing happens.

Why is that, one might wonder. Every function can be written as a power series. For \(sin\) the series looks like

The dimension of every term must be the same. The only way for that to be case is if the input \(x\) is dimensionless. Then so will the output.

The other functions can be written as similar power series and we’ll see on those too that the input and output must be dimensionless.

sinq :: (Floating v) => Quantity One v -> Quantity One v
sinq (ValQuantity dl v) = ValQuantity d1 (sin v)

cosq :: (Floating v) => Quantity One v -> Quantity One v
cosq (ValQuantity dl v) = ValQuantity d1 (cos v)

We quickly realize a pattern, so let’s generalize a bit.

qmap :: (a -> b) -> Quantity dim a -> Quantity dim b
qmap f (ValQuantity d v) = ValQuantity d (f v)

instance Functor (Quantity d) where
  fmap = qmap

qfold :: (a -> a -> b) -> Quantity dim a -> Quantity dim a -> Quantity dim b
qfold f (ValQuantity d v1) (ValQuantity _ v2) = ValQuantity d (f v1 v2)

sinq, cosq, asinq, acosq, atanq, expq, logq :: (Floating v) =>
  Quantity One v -> Quantity One v
sinq  = fmap sin
cosq  = fmap cos
asinq = fmap asin
acosq = fmap acos
atanq = fmap atan
expq  = fmap exp
logq  = fmap log

Why not make Quantity an instance of Num, Fractional and Floating? The reason is that the functions of those type classes have the following type

(*) :: (Num a) => a -> a -> a

which isn’t compatible with Quantity since multiplication with Quantity has the following type

(*#) :: (Num v) => Quantity d1 v -> Quantity d2 v ->
                   Quantity (d1 `Mul` d2) v

The input here may actually be of different types, and the output has a type depending on the types of the input. However, the kind of the inputs and output are the same, namely Quantity. We’ll just have to live with not being able to make Quantity a Num-instance.

However, operations with only scalars (type One) has types compatible with Num.

Exercise Quantity One has compatible types. Make it an instance of Num, Fractional and Floating.

instance (Num v) => Num (Quantity One v) where
  (+) = (+#)
  (-) = (-#)
  (*) = (*#)
  abs = fmap abs
  signum = fmap signum
  fromInteger n = ValQuantity V.one (fromInteger n)

instance (Fractional v) => Fractional (Quantity One v) where
  (/) = (/#)
  fromRational r = ValQuantity V.one (fromRational r)

instance (Floating v) => Floating (Quantity One v) where
  pi    = ValQuantity V.one pi
  exp   = expq
  log   = logq
  sin   = sinq
  cos   = cosq
  asin  = asinq
  acos  = acosq
  atan  = atanq
  sinh  = fmap sinh
  cosh  = fmap cosh
  asinh = fmap asinh
  acosh = fmap acosh
  atanh = fmap atanh

Syntactic sugar

In order to create a value representing a certain distance (5 metres, for example) one does the following

distance :: Quantity T.Length Double
distance = ValQuantity V.length 5.0

Writing that way each time is very clumsy. You can also do “dumb” things such as

distance :: Quantity T.Length Double
distance = ValQuantity V.time 5.0

with different dimensions on value-level and type-level.

To solve these two problems we’ll introduce some syntactic sugar. First some pre-made values for the 7 base dimensions and the scalar.

length :: (Num v) => Quantity Length v
length = ValQuantity V.length 1

mass :: (Num v) => Quantity Mass v
mass = ValQuantity V.mass 1

time :: (Num v) => Quantity Time v
time = ValQuantity V.time 1

Exercise Do the rest.

current :: (Num v) => Quantity Current v
current = ValQuantity V.current 1

temperature :: (Num v) => Quantity Temperature v
temperature = ValQuantity V.temperature 1

substance :: (Num v) => Quantity Substance v
substance = ValQuantity V.substance 1

luminosity :: (Num v) => Quantity Luminosity v
luminosity = ValQuantity V.luminosity 1

one :: (Num v) => Quantity One v
one = ValQuantity V.one 1

And now the sugar.

infixl 3 #
(#) :: (Num v) => v -> Quantity d v -> Quantity d v
v # (ValQuantity d bv) = ValQuantity d (v*bv)

The intended usage of the function is the following

ghci> let myDistance = 5 # length
ghci> :t myDistance
t :: Num v => Quantity Length v
ghci> myDistance
5 m

To create a Quantity with a certain value (here 5) and a certain dimension (here length), you write as above and get the correct dimension on both value-level and type-level.

This way of writing in Haskell is similiar to what you do in traditional physics.

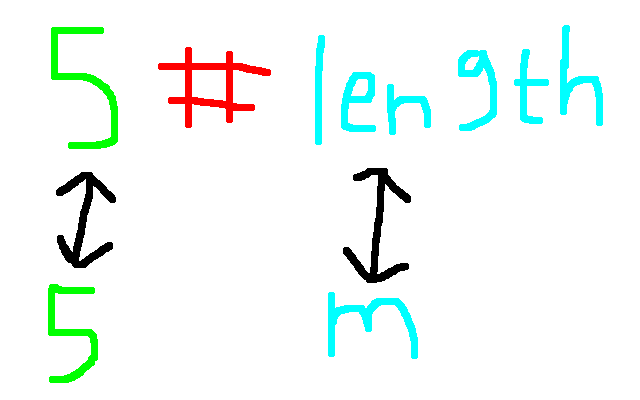
Both mean that “now we get 5 pieces of the SI-unit meters”. This is signified in the implementation by b*bv where bv stands for “base value”. The base value is the SI-unit, which is \(1\). Since “length” and “meter” are equivalent in our implementation, length means “meter”.

But let’s not stop there. It would be prettier if you could actually write meter instead of length. In fact, not much code is needed for this!

Exercise Make it so that one can write the SI-units instead of the base dimensions when one uses the sugar. Then show how to write \(4\) seconds.

meter    = length
kilogram = mass
second   = time
ampere   = current
kelvin   = temperature
mole     = substance
candela  = luminosity
unitless = one

fourSeconds = 4 # second

That’s nice and all, but we can actually take this way of thinking even further. The sugar-function # multiplies with the base value of a unit. Thanks to this, we can actually support more units than just the SI-units! (At least for input.)

Exercise Make it so that one can write units such as inch, foot and pound in the same way one can write the SI-units.

inch = 0.0254 # meter
foot = 0.3048 # meter
pound = 0.45359237 # kilogram

All right, so now we have tackled the problem of writing quantities easier than before. What about the second problem?

We want to maintain the invariant that the dimension on value-level and type-level always match. The pre-made values from above maintain it, and so do the arithmetic operations we previously created. Therefore, we only export those from this module! The user will have no choice but to use these constructs and hence the invariant will be maintained.

If the user needs other dimensions than the base dimensions (which it probably will), the follwing example shows how it’s done.

ghci> let myLength = 5 # length
ghci> let myTime = 2 # time
ghci> let myVelocity = myLength /# myTime
ghci> myVelocity
2.5 m/s

New dimensions are created “on demand”. Furthermore

ghci> let velocity = length /# time
ghci> let otherVelocity = 188 # velocity

it’s possible to use the sugar from before on user-defined dimensions.

Just for convenience sake we’ll define a bunch of common composite dimensions. Erm, you’ll define.

Exericse Define pre-made values for velocity, acceleration, force, momentum and energy.

velocity     = length   /# time
acceleration = velocity /# time
force        = mass     *# acceleration
momentum     = force    *# time
energy       = force    *# length

A physics example

To conclude this chapter, we show an example on how to code an exercise and its solution in this domain specific language we’ve created for quantities.

The code comments show what GHCi prints for that line.

The exercise is “A dog runs, jumps and lands sliding on a carriage. The dog weighs \(40 \, kg\) and runs in \(8 \, m/s\). The carriage weighs \(190 \, kg\). The coefficient of friction between the dog’s paws and the carriage is \(0.7\).”

This is illustrated in the painting below.

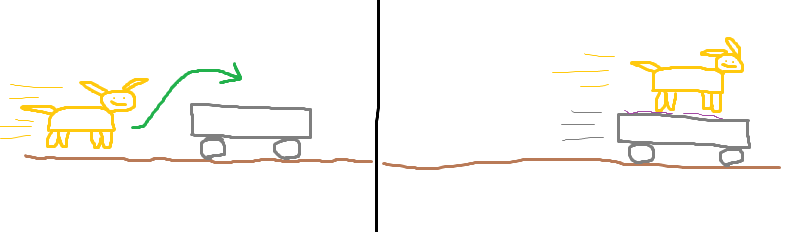
1. Calculate the (shared) final velocity of the dog and the carriage.

mDog      = 40 # mass    -- 40 kg
viDog     = 8 # velocity -- 8 m/s
mCarriage = 190 # mass   -- 190 kg
u         = 0.7 # one    -- 0.7

No external forces are acting on the dog and the carriage. Hence the momentum of the system is preserved.

piSystem = mDog *# viDog -- 320 kg*m/s
pfSystem = piSystem      -- 320 kg*m/s

In the end the whole system has a shared velocity of its shared mass.

mSystem  = mDog +# mCarriage   -- 230 kg
vfSystem = pfSystem /# mSystem -- 1.39 m/s

2. Calculate the force of friction acting on the dog.

fFriction = u *# fNormal        -- 275 kg*m/s^2
fNormal   = mDog *# g           -- 393 kg*m/s^2
g         = 9.82 # acceleration -- 9.82 m/s^2

3. For how long time does the dog slide on the carriage?

aDog = fFriction /# mDog -- 6.87 m/s^2

vDelta = mDog -# vfSystem

* Couldn't match type 'Numeric.NumType.DK.Integers.Neg1
                 with 'Numeric.NumType.DK.Integers.Zero
...

Whoops! That’s not a good operation. Luckily the compiler caught it.

vDelta = viDog -# vfSystem -- 6.60 m/s
tSlide = vDelta /# aDog    -- 0.96 s

Conclusion

Okay, so you’ve read a whole lot of text by now. But in order to really learn anything, you need to practise with some additional exercises. Some suggestions are

• Implement first value-level dimensions, then type-level dimensions and last quantites by yourself, without looking too much at this text.
• Implement a power function.
• Implement a square-root function. The regular square-root function in Haskell uses exp and log, which only work on Quantity One. But taking the the square-root of e.g. an area should be possible.
• Extending the Quantity data type here by adding support for prefixes and non-SI-units.
• Ditching the separate implementations of value-level and type-level, and only use one with Data.Proxy.

After reading this text and doing some exercies, we hope you’ve learnt

• The relation between dimensions, quantities and units.
• How dimensions…
  • …restrict operations such as comparsion to quantities of the same dimension.
  • …change after operations such as multiplication.
  • …can be implemented on the type-level in Haskell to enforce the two above at compile-time.
• The basics about kinds and type-level programming in Haskell.

Further reading

The package Dimensional inspired a lot of what we did here. Our Quantity is like a “lite” version of Dimensional, which among other things, support different units and use Data.Proxy.

The type-level progamming in this text was done with the help of the tutorial Basic Type Level Programming in Haskell. If you want to know more about kinds and type-level programming, it’s a very good starting point.